【摘要】到了高三总复习的时候发现有许多的数学知识点还没有理解,而这些知识点往往就是必考的知识点,www.kmf8.com对此做了相关的高三一轮数学知识点资料,请同学们参考学习!
棱锥具有的性质:
①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).
②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.
⑶特殊棱锥的顶点在底面的射影位置:
①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.
②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心.
③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心.
④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.
⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.
⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.
⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;
⑧每个四面体都有内切球,球心
![]()
是四面体各个二面角的平分面的交点,到各面的距离等于半径.
[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)
ii. 若一个三角锥,两条对角线互相垂直,则第三对角线必然垂直.
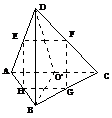
简证:AB⊥CD,AC⊥BD
![]()
BC⊥AD. 令
![]()
得
![]()
,已知
![]()
![]()
则
![]()
.
iii. 空间四边形OABC且四边长相等,则顺次连结各边的中点的四边形一定是矩形.
iv. 若是四边长与对角线分别相等,则顺次连结各边的中点的四边是一定是正方形.
简证:取AC中点
![]()
,则
![]()
平面
![]()
90°易知EFGH为平行四边形
![]()
EFGH为长方形.若对角线等,则
![]()
为正方形.
总结:www.kmf8.com整理的高三一轮数学知识点:棱锥的性质总结帮助同学们复习以前没有学会的数学知识点,请大家认真阅读上面的文章,也祝愿大家都能愉快学习,愉快成长!
相关阅读:备战最新高考第一轮复习资料精汇
浏览了本文的读者也浏览了:
- 高三一轮数学知识点:棱锥的性质总结
- › 高三一轮生物备考:植物对水分的吸收和利用
- › 高三一轮复习生物要点:首要任务是回归课本
- › 高三一轮复习:高考英语中最常考的状语从句
- › 高三一轮英语形容词和副词知识点
- › 高三一轮英语复习方法指导
- › 2016英语高三一轮复习要点归纳
- › 高三一轮复习英语要点:英语介词
- › 2016年英语高三一轮复习方案
- › 2016高三一轮复习数学立体几何复习方法
- › 高三一轮复习数学:如何提升效率
- › 高三一轮数学复习资料:一元二次不等式及其解法
- › 高三一轮数学复习资料:算术平均数
- 在百度中搜索相关文章:高三一轮数学知识点:棱锥的性质总结
- 在谷歌中搜索相关文章:高三一轮数学知识点:棱锥的性质总结
- 在soso中搜索相关文章:高三一轮数学知识点:棱锥的性质总结
- 在搜狗中搜索相关文章:高三一轮数学知识点:棱锥的性质总结
