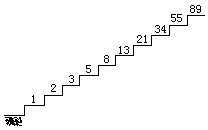
其中从第三个数起,每个数都是它前面两个数之和。登上第10级台阶的方法数对应这串数的第10个,即89。也可以在图上直接写出计算得出的登上各级台阶的方法数(见下图)。
5、
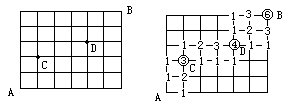
在左下图中,从A点沿实线走最短路径到B点,共有多少条不同路线?

分析与解:题目要求从左下向右上走,所以走到任一点,例如右上图中的D点,不是经过左边的E点,就是经过下边的F点。如果到E点有a种走法(此处a=6),到F点有b种走法(此处b=4),根据加法原理,到D点就有(a+b)种走法(此处为6+4=10)。我们可以从左下角A点开始,按加法原理,依次向上、向右填上到各点的走法数(见上图),最后得到共有35条不同路线。
6、下图是某街区的道路图。从A点沿最短路线到B点,其中经过C点和D点的不同路线共有多少条?
分析与解:本题可以同例2一样从A标到B,也可以将从A到B分为三段,先是从A到C,再从C到D,最后从D到B。如上图所示,从A到C有3种走法,从C到D有4种走法,从D到B有6种走法。因为从A到B是分几步走的,所以应该用乘法原理,不同的路线共有
3×4×6=72(条)。
7、沿左下图中箭头所指的方向从A到B共有多少种不同的走法?

分析与解:如右上图所示,先标出到C点的走法数,再标出到D点和E点的走法数,然后标出到F点的走法数,最后标出到B点的走法数。共有8种不同的走法。
8、有15根火柴,如果规定每次取2根或3根,那么取完这堆火柴共有多少种不同取法?
分析与解:为了便于理解,可以将本题转变为“上15级台阶,每次上2级或3级,共有多少种上法?”所以本题的解题方法与例1类似(见下表)。


注意,因为每次取2或3根,所以取1根的方法数是0,取2根和取3根的方法数都是1。取4根的方法数是取1根与取2根的方法数之和,即0+1=1。依此类推,取n根火柴的方法数是取(n-3)根与取(n-2)根的方法数之和。所以,这串数(取法数)中,从第4个数起,每个数都是它前面第3个数与前面第2个数之和。取完15根火柴共有28种不同取法。
相关推荐
2014年寒假作文、日记大全
六年级奥数加法原理知识点讲解
www.kmf8.com- 小学计数问题之加法原理练习题及答案
- › 小学计数问题之加法原理练习题及答案
- › 小学计数问题乘法原理练习题含答案
- › 小学计数之捆绑法的经典例题解析
- › 小学计数凑元素选板法的例题讲解
- 在百度中搜索相关文章:小学计数问题之加法原理练习题及答案
- 在谷歌中搜索相关文章:小学计数问题之加法原理练习题及答案
- 在soso中搜索相关文章:小学计数问题之加法原理练习题及答案
- 在搜狗中搜索相关文章:小学计数问题之加法原理练习题及答案
