0的各年龄组的人数大部分随年龄减小而减小。④峰型：小于平均寿命的某一年龄区间的各组人数显著超过基准值
(
)，达到
(
)的1.5倍以上者称为强峰型。峰型、特别是强峰型人口状态可能对社会经济生活产生严重影响。图2[ 1978年中国年龄分布曲线图]
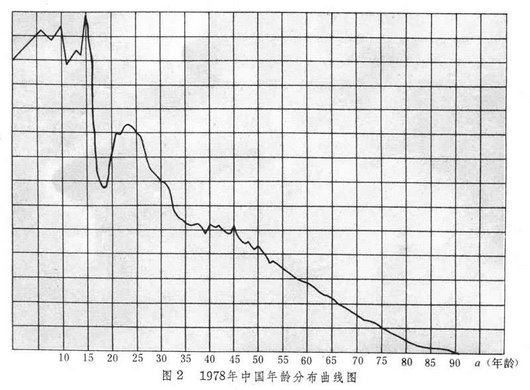
是1978年中国年龄分布曲线,在0～18岁和19～30岁分别有两个峰，约为
(
)的1.5～2倍。⑤谷型：在某一年龄区间各年龄组人数显著小于
(
)，这说明由于某种社会因素使这些年龄组在过去某些年代死亡率很高，它与峰型一样会带来不利的影响。⑥振荡型：在小于平均寿命的区间有二个以上的脉冲式峰和谷相间出现，它的不利影响比脉冲式单峰或单谷更为严重，是应该尽力避免的。
人口指数 为了定量研究人口问题，常需要一些人口数值特征量，如出生率、死亡率、自然增长率、人口总数、劳动力总数和平均期望寿命等。这些特征量通常称为人口指数。每一项人口指数只是从某一个方面定量表示人口的当前状态和发展过程的特征。例如，出生率反映生育水平，死亡率反映死亡水平，自然增长率反映人口增长速度。人口指数可以分为静态指数和动态指数两类。前者描述社会人口当前状态或某一特定年代的人口状态;后一类则描述人口状态变化的动态特性，如人口纯再生产率、妇女两代间隔、人口总数翻一番所需时间等。人口指数既可以通过公式计算，也可通过人口普查或抽查由实际统计数据得到。
人口系统稳定性理论 人口系统是一个带有正反馈的动态系统，因而存在着李雅普诺夫稳定性问题。在人口控制论中，宋健等人用半群理论首次证明，对于任一定常人口系统(见定常系统)，都存在一临界妇女总和生育率βcr：
[365-01]
式中K(
)、
(
)和
上一页 [1] [2] [3] [4] [5] [6] 下一页
Tag:数学知识，数学知识大全，初中学习网 - 数理化百科 - 数学知识
- 关于人口控制论的数学百科大全
- › 关于人口控制论的数学百科大全
- 在百度中搜索相关文章：关于人口控制论的数学百科大全
- 在谷歌中搜索相关文章：关于人口控制论的数学百科大全
- 在soso中搜索相关文章：关于人口控制论的数学百科大全
- 在搜狗中搜索相关文章：关于人口控制论的数学百科大全