![]()
为决策变量,
![]()
为决策变量数,
![]()
为目标个数;
![]()
![]()
![]()
为技术系数,
![]()
![]()
为第
![]()
种有限资源量,L为有限资源个数。
例如,某工业企业欲在计划期内生产A、B两种产品,其单位产品所需设备台时、材料及利润汇总如下表:[]
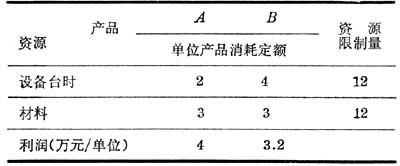
若工厂决策者只要求获取最大利润这一目标,则可用线性规划求解,求得最优解
![]()
=(4,0,4,0),即A产品生产4个单位,B产品不生产,设备台时剩余4个单位,材料正好用完,所获最大利润为4×4=16万元。但决策者认为还应顾及满足社会需求的目标,并依次确定三个优先次序
![]()
1、
![]()
2和
![]()
3。①
![]()
1:在计划期间内工厂获利至少在12万元以上,求解minp1(
![]()
![]()
),即要求达不到利润目标值的负偏差量最小。②p2:要求A产品的数量为 B产品的1.5倍,求解minp2(
![]()
![]()
上一页 [1] [2] [3] [4] [5] [6] 下一页
Tag:数学知识,数学知识大全,初中学习网 - 数理化百科 - 数学知识
- 目标规划模型——经典数学
- › 目标规划模型——经典数学
- 在百度中搜索相关文章:目标规划模型——经典数学
- 在谷歌中搜索相关文章:目标规划模型——经典数学
- 在soso中搜索相关文章:目标规划模型——经典数学
- 在搜狗中搜索相关文章:目标规划模型——经典数学
