![]()
=0,
![]()
![]()
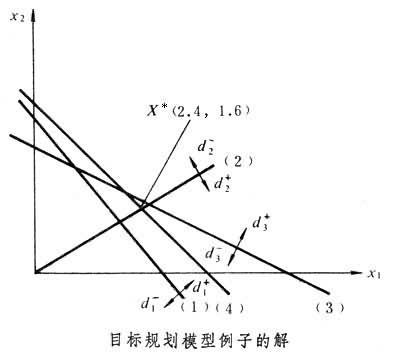
=0.8,即A产品生产2.4单元,B产品生产1.6单元,利润目标超额 2.72万元,A产品为B产品的1.5倍,设备台时剩余0.8单位,即Z=0+0+0.8=0.8为最小。
在一般情况下,可在目标规划求解之前,先用线性规划求出主要目标的最优解,作为最优平衡的大致界限,再用目标规划进行调整,可用单纯形法通过电子计算机求解模型,根据求解结果分析目标值和实际值产生差距的原因,并提出相应的措施,最终求得满意解为止。
[目标规划模型例子的解]
www.kmf8.com提供的目标规划模型——经典数学,希望给大家的学习生活增添色彩~~
Tag:数学知识,数学知识大全,初中学习网 - 数理化百科 - 数学知识
- 目标规划模型——经典数学
- › 目标规划模型——经典数学
- 在百度中搜索相关文章:目标规划模型——经典数学
- 在谷歌中搜索相关文章:目标规划模型——经典数学
- 在soso中搜索相关文章:目标规划模型——经典数学
- 在搜狗中搜索相关文章:目标规划模型——经典数学
