www.kmf8.com
15. 如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7= .
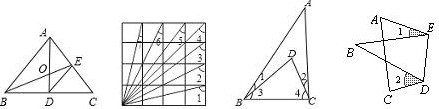
第11题图 第15题图 第16题图 第17题图
16.如图,∠1=20°,∠2=25°,∠A=35°,则∠BDC= .
17.如图所示,将△ABC沿着DE翻折,若∠1+∠2=70°,则∠B= 度.
18. 如图,AM,CM分别平分∠BAD和∠BCD. 求证:∠M= 0.5(∠B+∠D).
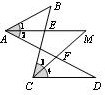
19.如图⑴,△ABC中,AD是角平分线,AE⊥BC于点E.
⑴若∠C=80°,∠B=50°,求∠DAE的度数.⑵若∠C>∠B,求证:∠DAE= 0.5(∠C-∠B).
⑶如图⑵若将点A在AD 上移动到A?处,A?E⊥BC于点E.此时∠DAE变成∠DA?E,⑵中的结论还正确吗?为什么?⑷将图中的AE改为垂直于AD的直线,此时图中的∠DAE??=0.5(∠C-∠B)吗?
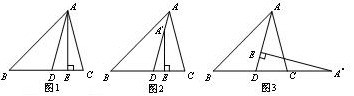
八.三角形外角定理及推论:三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任何一个内角.
20.如图,∠A+∠B+∠C+∠D+∠E+∠F= .
21.如图,CD平分△ABC的外角∠ACE,求证:∠BAC>∠B.
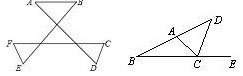
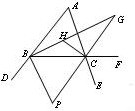
22.如图,BH、CH分别平分∠ABC、∠ACB,BP、CP分别平分∠DBC、∠ECB, BH、PC交于点G,求证:⑴∠HBP=∠HCP=90°;⑵∠G= ∠A;⑶分别探索∠BHC、∠P与∠A的数量关系.
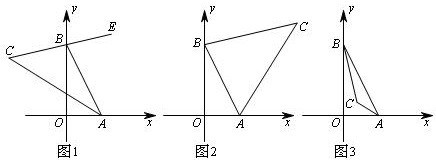
23.⑴如图1,∠xOy=90°,点A、B分别在射线Ox、Oy上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.⑵如图2,如果BC、AC分别是∠ABx、∠BAy的平分线,问:B、A在Ox、Oy上运动过程中,∠C的度数是否改变?若不改变,求出其值;若改变,说明理由.⑶如图3,若BC、AC分别是∠BAO的平分线,问:B、A在Ox、Oy上运动过程中,∠C的度数是否改变?⑷若图中∠AOB=70°,以上图中∠C的度数又分别是多少?
九
.多边形的对角线:从n边形的一个顶点可以引n-3条对角线,将多边形分成n-2个三角形。n边形共有0.5n(n-3)条对角线。
24.若凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是 .
25.过m边形的一个顶点有4条对角线,n边形没有对角线,p边形有p条对角线,则(m-p)n= .
十.多边形的内角和与外角和:多边形的内角和等于(n-2)180°(n≥3).多边形的外角和等于360°.
26.若一个n边形的内角和为720°,则边数n= .
27.若一个正多边形的一个外角等于40°,则这个多边形是 边形.
28.如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了 米.
- 《三角形》知识要点与精析精练
- › 《三角形全等的条件》(第1课时)
- › 《三角形全等的条件》(第5课时)
- › 《三角形内角和》教学设计及反思
- › 《三角形的分类》教学案例与反思
- › 《三角形认识》案例与反思
- › 《三角形的内角和》教学后反思
- › 《三角形的认识》说课稿
- › 《三角形的内角和》反思
- › 《三角形的内角和》教后反思
- › 《三角形的分类》教后反思
- › 《三角形的高》教后反思
- › 《三角形的认识》教后反思
- 在百度中搜索相关文章:《三角形》知识要点与精析精练
- 在谷歌中搜索相关文章:《三角形》知识要点与精析精练
- 在soso中搜索相关文章:《三角形》知识要点与精析精练
- 在搜狗中搜索相关文章:《三角形》知识要点与精析精练
