www.kmf8.com
(3)两个完全一样的梯形,除了可以拼成平行四边形外,还可以拼成什么图形?
两个完全一样的直角梯形,可以拼成长方形;两个完全一样的直角梯形,上底与下底的和等于高时,可以拼成正方形。
(4)圆的面积公式是如何推导出S=Л×r2
因为拼成的平行四边形的底是圆周长的一半,而高是圆的半径,周长的一半就是Лr,所以面积就是Лr×r=Л×r2
(5)圆可不可以拼成正方形?
不能,因为拼成的平行四边形的底是圆周长的一半,而高是圆的半径,底永远是高的Л倍。
(通过磨课发现,学生出现的问题,多集中在这几点上,然而这几个知识点的处理对于下面构建框架图是很有必要的)
(设计意图:在初次汇报的基础上,再次进行讨论汇报,目的是使学生更好地理解平面图形周长和面积公式的推导过程,并且对于某些特殊情况进行补充,以达到复习巩固的目的)
四、梳理图形间的关系:
师:从他们组的介绍当中,有没有发现他们的推导过程体现着图像间的内在联系,课前还要求同学们根据面积公式的推导过程梳理了它们之间的关系,(课件出示:第三个任务)小组内再互相的说一说,根据他们的介绍可以进一步进行补充。
生:……(小组活动,梳理框架图,重点说根据什么这样梳理?)
师:哪个小组把你们的想法给大家说一说?
生:正方形的面积是根据长方形的面积推导出来的,平行四边形的面积是根据长方形或正方形的面积推导出来的,三角形和梯形、圆形的面积是根据平行四边形的面积推导出来的。
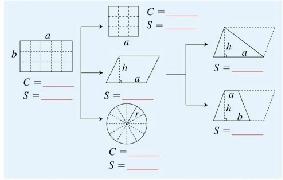
引导学生根据刚才的面积公式的推导过程进行补充。
师:刚才大家所说的,都是根据刚才推导过程中的发现。这样我们就可以将关系图进一步明确。(借助黑板上的模型梳理关系图)
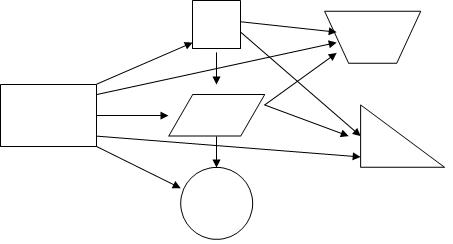
(借助模型在黑板上去构建框架图,这样更加直观,更利于学生的理解和交流)
(设计意图:通过初次汇报,使学生对平面图形的周长和面积的计算公式和内部关系初步感知,为下面的拓展和练习做准备)
五、公式的统一:
师:刚才我们结合推倒过程梳理了图形间的关系,不知道大家注意到了没有,这些平面图形中,除了由曲线围成的圆以外,剩下的五个图形的面积公式可不可以统一成一种图形的面积公式呢?
生:(独立思考)
师:谁来说说你的想法?(学生可能会有以下几种想法:)
生1:长方形,因为正方形是一个特殊的长方形,可以用长方形的面积公式,而平行四边形沿高剪下,可以拼成一个长方形,而三角形与梯形虽然说要除以2,单也可以变成长方形。
生2:平行四边形的面积
师:但我也有我自己的想法,大家想知道吗?(课件)大家仔细观察,这是什么图形?(梯形)看发生了什么变化?(变成三角形了)也就是说变成了一个上底为(0)的特殊的梯形,在仔细观察发生什么变化?(长方形),现在变成了一个上底和下底相等的特殊梯形,那这个呢?(平行四边形)。
现在你再想想可以统一成那个图形的公式呢?板书:
s=(a+a)b÷2
=2ab÷2
=ab
s=(a+0)b÷2
=ab÷2
师:面积公式可以统一成梯形面积的公式,这恐怕是大家没有想到的。看来平面图形的周长和面积中蕴含着丰富的知识等待着我们去发现。
(这一部分是本节课的一个升华,也是难点。即使让学生小组去讨论,理解起来有一定的难度,所以让学生直接独立思考,把自己的第一感受说出来。其实这里并没有真正意义上的对与错,学生说出是长方形或平行四边形,正是由于他们理解了根据面积公式推导过程构建的图形间的关系。而后教师借助课件演示引导学生初步感知。)
(设计意图:将平面图形的面积除圆之外都概括成一种图形的面积公式,目的并不是真正的统一,而是训练学生观察图形间、知识间的联系,从而发展学生的创造性思维)
六、巩固练习:
1、师:请大家仔细看这两组图形,认真审题,每组中的两个图形的周长和面积相等吗?(课件)
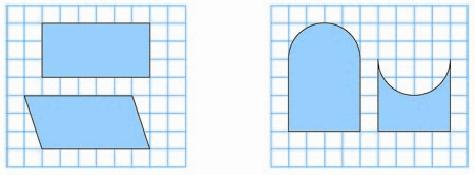
师:有想法了吗?谁来说一说?
生:1、周长不等,面积相等
2、周长相等,面积不等,因为……
那下面这两道题对吗?
1.如果两个平面图形的周长相等,则它们的面积一定相等。
2.如果两个平面图形的面积相等,则它们的周长一定相等。
(借助上面的习题,让学生进一步感知周长相等的图形面积不一定相等,面积相等的图形周长不一定相等。)
2.师:大家仔细看,把一个长方形拉成一个平行四边形,长方形和平行四边形的周长和面积不变,对不对呢?

生:不对,周长不变,面积变了,因为底没变,高缩小了。
3.判断:
(1)三角形的面积等于平行四边形面积的一半。
(2)同底等高的三角形,他们的形状不一定相等,但面积一定相等。
(3)半径是2厘米的圆,周长和面积相等。
(设计意图:通过有针对性、有梯度的练习让学生应用所学的知识解决实际问题,让学生更好地理解和掌握)
师:看来我们在面对这类问题是,还要灵活的运用。
- 《平面图形的周长和面积的复习课》教案
- › 《平面图形的周长和面积的复习课》教案
- 在百度中搜索相关文章:《平面图形的周长和面积的复习课》教案
- 在谷歌中搜索相关文章:《平面图形的周长和面积的复习课》教案
- 在soso中搜索相关文章:《平面图形的周长和面积的复习课》教案
- 在搜狗中搜索相关文章:《平面图形的周长和面积的复习课》教案
