有些数量关系比较复杂的应用题,按常规思路解答,往往不易解出。如果从特殊的角度来分析、思考,却能化繁为简,由难变易,使所求问题顺利获解。教会学生一些特殊解题思路,有利于发展学生智力,培养学生分析问题和解决问题的能力。本文介绍八种特殊解题思路,仅供同行参考。
一、假设思路
运用“假设”的方法,可以使解题思路通畅。
例如:甲、乙两个仓库储存粮食重量的比是10:9,如果甲仓库运出粮食储存量的20%,乙仓库运进粮食12吨,那么乙仓库的粮食就比甲仓库多24吨,甲仓库原有粮食多少吨?
我们先假设乙仓库没有运进12吨粮食。那么,从甲仓库运出粮食储存量的20%,乙仓库的粮食只比甲仓库多24-12=12(吨)。这样,数量关系就显得简单明了。由“甲仓库运出粮食储存量的20%”,可得这时甲乙两仓库储存粮食重量的比为[10×(1-20%)]:9=8:9。比的份数,乙比甲多9-8=1(份)。这1份,就是乙仓库的粮食比甲仓库多的12吨。因此,从原来甲、乙两仓库储存粮食重量的比,可求得甲仓库原有粮食为12×10=120(吨)。
二、逆推思路
从应用题最后问题出发,由后而前地推算,便能顺利解答。
例如:一根绳子,第一次剪去全长的1/4又1/4米,第二次剪去余下的1/3又1/3米,第三次剪去再余下的1/2又1/2米,还剩下5米。这根绳子长多少米?
这道题,顺着已知条件思考,比较困难。我们可以从后逐步向前推算:最后剩下的5米加上1/2米,即5(1/2)米,正好是第三次余下的1-1/2=1/2,由此可推得第二次余下5(1/2)÷1/2=11(米)。11米加上1/3米,即11(1/3)米,正好是第一次剪去后余下的1-1/3=2/3,由此可推得第一次余下的是11(1/3)÷2/3=17(米)。17米加上1/4米,即17(1/4)米,正好是原长的3/4,从而可推得这根绳子原长为17(1/4)÷3/4=23(米)。
三、联想思路
“联想”是由一事物想起另一事物的心理过程。教会学生“联想”的方法,可以使学生的思维更加广阔和灵活。
例如:幼儿园买来红皮球和白皮球,红皮球占皮球总只数的5/9,后来又买来20只红皮球,这时红皮球正好占皮球总只数的60%,现在有红皮球多少只?
由“红皮球占皮球总只数的5/9”,联想到红皮球占5份,白皮球占4份;由“后来又买来20只红皮球,这时红皮球正好占皮球总只数的60%”,联想到现在皮球总只数中,红皮球占6份,白皮球占4份。这时可知,白皮球占的份数不变,红皮球增加6-5=1(份)。之所以增加了1份,是因为增加了20只红皮球,所以1份就是20只皮球。红皮球这时占6份就是20×6=120(只),白皮球占4份就是20×4=80(只)。
四、转化思路
有的应用题,将数量关系进行适当转化,可以使问题变得简单,容易求解。
例如:两江机器制造厂有四个车间,第一车间人数是二、三、四车间人数的1/2,第二车间人数是一、三、四车间人数的1/3,第三车间人数是一、二、四车间人数的1/4第四车间有260人。问第一、二、三车间各有多少人?
这道题里的三个分数依据的单位“1”都不同。对此,我们可将“第一车间人数是二、三、四车间人数的1/2”转化为“第一车间人数是四个车间总人数的1/(2+1)=1/3”,将“第二车间人数是一、三、四车间人数的1/3”转化为“第二车间人数是四个车间总人数的1/(3+1)=1/4”,将“第三车间人数是一、二、四车间人数的1/4”转化为“第三车间人数是四个车间总人数的1/(4+1)=1/5”。三个分数依据的单位“1”统一了,即可求出四个车间的总人数为:260÷(1-1/(2+1)-1/(3+1)-1/(4+1))=1200(人)。由此可求出第一车间有1200×1/3=400(人),第二车间有1200×1/4=300(人),第三车间有1200×1/5=240(人)。
五、代换思路
有的应用题中的数量关系比较隐蔽,我们可以根据题目中所给的条件,用一个具体数量代换一个未知量,从而使问题很快求解。
例如:有一段钢材,横截面是正方形,它的面积是40平方厘米,现要把它加工成一种 www.kmf8.com 零件,形状如下图所示,求阴影部分面积。
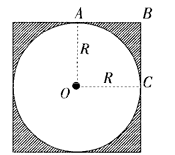
这道题,根据已知条件直接解答比较困难,若用“代换”的方法来思考,就比较容易解答。设图中圆的半径为R厘米,那么小正方形AOCB的面积为40÷4=10(平方厘米),扇形AOC的面积为
所以右上角阴影部分的面积为10-7.85=2.15(平方厘米),由此得出原来图中阴影部分的面积为2.15×4=8.6(平方厘米)。
六、类推思路
有些应用题虽然叙述的事情不同,但实质一样,因此我们可以运用“类推”的方法解答。
例如:1.一件工程,由甲工人单独做需30天完成,由乙工人单独做需20天完成,甲乙两个工人合做,需要多少天完成?
2.一辆客车从A城开往B城需30小时,一辆货车从B城开往A城需20小时。客车和货车同时从A、B两城相对开出,几小时后两车在途中相遇?
第1题,可根据“工作总量一工作效率=工作时间”的关系式列出算式:1÷(1/30+1/20)=12(天)。
第2题,我们可以把A、B两城之间的路程看作工作总量“1”,把客车和货车每小时行全路程的几分之几分别看作工作效率“1/30”与“1/20”。要求两车几小时相遇,可根据第1题的关系式类推,列出相同的算式。
七、比较思路
有的应用题可以通过比较题中的已知条件,找出对应数量的差,分析研究数量差的变化情况,从而找到解题方法。
例如:买2本故事书和3支钢笔共用去17.60元,买同样的4本故事书和5支钢笔共用去30.40元。求每本故事书和每支钢笔的价钱。
根据题意列出条件比较:
2本故事书——3支钢笔——17.60元
4本故事书——5支钢笔——3040元
因为两次买的故事书本数、钢笔支数以及钱数都没有“相同量”,不容易比较对应数量差的关系。为此,我们可以将第一次买的故事书本数、钢笔支数和共用去的钱数,同时扩大2倍,即:
4本故事书——6支钢笔——3520元
Tag:解题研究,小学数学教学,小学数学教学网,小学数学教学 - 解题研究
- 教会学生特殊解题思路
- › 教会学生学会学习的方法反思
- › 教会学生特殊解题思路
- 在百度中搜索相关文章:教会学生特殊解题思路
- 在谷歌中搜索相关文章:教会学生特殊解题思路
- 在soso中搜索相关文章:教会学生特殊解题思路
- 在搜狗中搜索相关文章:教会学生特殊解题思路
